Anyone who has been reading this blog regularly knows that at GoDataDriven we love open source. With this we usually imply technology, but what about the data? Recently I discovered Kaggle as a great source of fun, open datasets. As a board game enthusiast I was happy to find a dataset exported from BoardGameGeek.com, a board game review site. The set contains average ratings of boardgames. It also contains some boardgame metadata such as category and year of publication.
In this post I will share my experiences exploring the data set and my attempt to reverse engineer the secret rating algorithm of BoardGameGeek. I did the analysis in R and I will show the code along the way.
Common issues with average ratings
First of all, let’s load our data and exclude games without Bayesian averages.
library(tidyverse) library(modelr) boardgames_tbl read_csv('./games.csv') %>% mutate(sum_ratings = users_rated * average_rating, has_average_rating = average_rating !=0, has_bayes_average_rating = bayes_average_rating != 0) %>% filter(has_average_rating) with_bayes_average boardgames_tbl %>% filter(bayes_average_rating != 0)
A common problem with average ratings is that items with few votes tend to assume extreme scores. We see this also in the boardgame set. Extreme scores happen at the left of the spectrum. With more votes the score variance narrows considerably.
ggplot(boardgames_tbl, aes(users_rated, average_rating)) + geom_point(alpha = 0.1) + ggtitle('[1] Games with few votes tend to have extreme ratings.')
Is this a bad thing? Most likely you are using a site like BoardGameGeek to do one of two things:
- looking up the score of a game
- discovering new games by exploring the top
Extreme scores don’t exactly help here. You might buy a game with an amazing score only to find out it is not that interesting. Or in the case of a low rating you might miss out on a great opportunity!
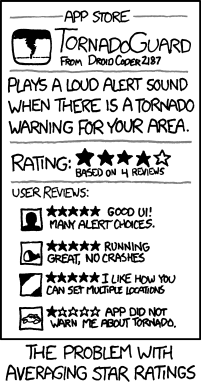
Maybe you want to explore the best boardgames but instead you find the top 100 filled with 10/10 scores. Experience many such false positives and you will lose faith in the rating system. Let’s be clear this isn’t exactly incidental either: most games have relatively few votes and suffer from this phenomenon.
The Bayesian average
Fortunately, there are ways to deal with this. BoardGameGeek’s solution is to replace the average by the Bayesian average. In Bayesian statistics we start out with a prior that represents our a priori assumptions. When evidence comes in we can update this prior, computing a so called posterior that reflects our updated belief.
Applied to boardgames this means: if we have an unrated game we might as well assume it’s average. If not, the ratings will have to convince us otherwise. This certainly removes outliers as we will see below!
with_bayes_average_long with_bayes_average %>%
gather(metric, rating, average_rating, bayes_average_rating)
ggplot(with_bayes_average_long, aes(users_rated, rating)) +
geom_point(alpha = 0.1) +
facet_grid(. ~ metric) +
ggtitle('[2] The Bayesian average removes outliers.')
Another common problem is that relatively new items tend to have higher ratings. We can see clearly how the average score of boardgames has increased over time.
agg with_bayes_average %>%
group_by(yearpublished) %>%
summarise(mean_average = mean(average_rating),
mean_nvotes = mean(users_rated),
n = n()) %>%
filter(n > 10, yearpublished != 0)
ggplot(agg, aes(yearpublished, mean_average, size = mean_nvotes)) +
geom_point() +
geom_smooth() +
ggtitle('[3] On average recently published games have higher ratings.')
Although it is possible that gamemakers finally understand how to make proper games, it is more likely something else is at play. It might be that enthusiasts are the first to go out and buy a game. Perhaps early adopters hand out higher votes in general. Anyway it is nice to see that the Bayesian average also moderates this effect somewhat.
agg with_bayes_average %>%
group_by(yearpublished) %>%
summarise(mean_average = mean(average_rating),
mean_bayes_average = mean(bayes_average_rating),
n = n()) %>%
filter(n > 10, yearpublished > 1960) %>%
gather(type, mean_average, mean_average, mean_bayes_average)
ggplot(agg, aes(yearpublished, mean_average, weight=n, color = type)) +
geom_point(alpha = 0.3) +
geom_smooth() +
ggtitle('[4] The Bayesian average moderates the recency effect.')
But how do we get from average rating to its Bayesian counterpart? After all, a quick plot shows these two scores are quite different.
with_bayes_average boardgames_tbl %>% filter(bayes_average_rating != 0)
ggplot(with_bayes_average, aes(bayes_average_rating, average_rating)) +
geom_point(alpha = 0.1) +
ggtitle('[5] The normal average and the Bayesian average are not much alike.' )
It turns out the Bayesian average can be computed after collecting all votes. It is as if one were to add (C) dummy voters that on average vote an (m) score.
But what are the values of (C) and (m)? In [2] we saw that the Bayesian average of games with few votes appear to be in the 5-7 score range. Let’s divide all averages into two groups based on whether their normal average is larger than 5.5. It turns out the peaks of these two groups fall slightly left and right of the 5.5 Bayes score. As most games have few votes, the prior is probably close and in between these peaks. This suggests 5.5 as a point of departure, which would make sense: a priori it is most likely a game is average. Also, we might want center the scale and place average games at the midpoint.
ratings with_bayes_average %>% mutate(above_average = average_rating >= 5.5)
ggplot() +
geom_density(aes(bayes_average_rating, y = ..scaled.., fill=above_average), alpha = 0.3, data = ratings) +
ggtitle('[6] The prior score appears to be at the 5.5 midpoint.' )
Reverse engineering the algorithm
If you still don’t believe (m = 5.5) you could always check the BoardGameGeek FAQ:
To prevent games with relatively few votes climbing to the top of the BGG Ranks, artificial “dummy” votes are added to the User Ratings. These votes are currently thought to be 100 votes equal to the mid range of the voting scale: 5.5, but the actual algorithm is kept secret to avoid manipulation. The effect of adding these dummy votes is to pull BGG Ratings toward the mid range. Games with a large number of votes will see their BGG Rating alter very little from their Average Rating, but games with relatively few user ratings will see their BGG Rating move considerably toward 5.5.
It states that (m = 5.5) and (C = 100). Curiously, this does not correspond to the data.
m = 5.5 C = 100 faq_preds with_bayes_average %>% mutate(pred = (C*m + users_rated * average_rating) / (C + users_rated), resid = pred - bayes_average_rating) ggplot() + geom_point(aes(pred, bayes_average_rating), data=faq_preds, alpha=0.1) + ggtitle("[7] The FAQ formula does not correspond to the data.")
If you read closely, the FAQ actually states the real thing is slightly different.
…but the actual algorithm is kept secret to avoid manipulation.
Sounds like a challenge! We can write a cost function that computes the Bayesian average given the parameters (C) and (m) and returns the Mean Absolute Error.
f = function(C, m){ with_bayes_average %>% mutate(pred = (C*m + users_rated * average_rating) / (C + users_rated), resid = pred - bayes_average_rating) %>% summarise(mae = resid %>% abs %>% mean) %>% .[['mae']] }
Exploring the search space we find that the best fit appears to be at 750 dummy votes – unlike the suggested (100) dummy votes.
C_interval seq(1,2000, 10)
m_interval seq(4, 7, 0.1)
input_space = expand.grid(C = C_interval, m = m_interval)
space = input_space %>% rowwise %>% mutate(y = f(C, m))
ggplot(space, aes(C, m, fill=y)) +
geom_tile() +
scale_fill_gradientn(colours = rainbow(5)) +
ggtitle('[8] The best fit appears to be at 750 dummy votes.')
We can find the exact value with a nice little function called optimise. Given a function that returns a metric and a parameter space to explore, optimise returns the parameters for which the error is the least.
optimise(f, interval= c(1, 2000), m=5.5)
$minimum [1] 725.6158 $objective [1] 0.01206334
Perhaps the real number of dummy votes is more in the order of 725. At least this fits our data much neater!
m = 5.5 C = 725 optim_preds with_bayes_average %>% mutate(pred = (C*m + users_rated * average_rating) / (C + users_rated), resid = pred - bayes_average_rating) ggplot() + geom_point(aes(pred, bayes_average_rating), data=optim_preds, alpha=0.1) + ggtitle('[9] Assuming 725 dummy votes results in a neater fit.')
Conclusion
The predicted scores are not an exact reconstruction of the Bayes scores so I expect BoardGameGeek actually weighs in some other factor. Nevertheless, it seems that a stronger smoothing is applied than suggested. In conclusion, the Bayesian average certainly is an elegant additive smoother.





