In today’s high pace user experience it is expected that new recommended items appear every time the user opens the application, but what to do if your recommendation system runs every hour or every day? I give a solution that you can plug & play without having to re-engineer your recommendation system.

The common practice to update recommended items is to have the recommendation system re-score the available items every period of time T. This means that for a whole period T, the end-user faces the same content in the application’s entry screen. In today’s high pace user experience if T is even a few hours, let alone a day, the user can get bored of the same content displayed every time it opens the application during the period T. There can be many ways this scenario can happen but imagine the user opens the application and doesn’t like the recommended items and is too lazy or busy to scroll or search for something else. If the user opens the application again some minutes later to find exactly the same content as before this might have a big (negative) impact on the retention for this user.
An obvious solution to this problem is to shuffle the content in such a way that it remains relevant to the user while new content appears on the screen each time the user re-opens the application.
Below there are two screen shots from my YouTube account a couple of seconds apart with no interaction, just clicking the refresh button. We can notice several things:
- Content is still relevant.
- Content is not the same.
- Some content has changed position.
- Some new content has appeared.


This can be because YouTube re-scores items in a very short time T or runs an online algorithm.1 What can you do to achieve something similar if your recommendation system has a T in the order of hours?
In this blog post, I propose a simple solution based on a non-uniform shuffling algorithm that you can basically plug & play or build on top off.
Example scenario
Suppose you have 10,000 items in total that can be recommended to your user, you run the recommendation system over all the items and those 10,000 items get ranked in order of relevance of the content.2
The application shows 5 items on the entry screen. The first time the user opens the application after the re-scoring process the top 5 ranked items are shown. It is decided that from now on (based on user control groups, investigation, AB testing, etc.) until the next re-scoring process the entry screen should not be the same every time and remain relevant for the user.
Based on an investigation from the data scientist it turns out that somewhat relevant items appear until item 100.3 Then the idea is to somehow shuffle those 100 items such that the top 5 items shown are still relevant but not the same.
In order for the figures of this blog post to be more readable and understandable, I’ll use a hypothetical threshold of 20 items and not 100.
Fisher–Yates shuffle / uniform
Shuffling in Python is a very common action and can be done using the random module which contains the shuffle function.
>>> print(inspect.getsource(random.shuffle)) def shuffle(self, x, random=None): """Shuffle list x in place, and return None. Optional argument random is a 0-argument function returning a random float in [0.0, 1.0); if it is the default None, the standard random.random will be used. """ if random is None: randbelow = self._randbelow for i in reversed(range(1, len(x))): # pick an element in x[:i+1] with which to exchange x[i] j = randbelow(i+1) x[i], x[j] = x[j], x[i] else: _int = int for i in reversed(range(1, len(x))): # pick an element in x[:i+1] with which to exchange x[i] j = _int(random() * (i+1)) x[i], x[j] = x[j], x[i]
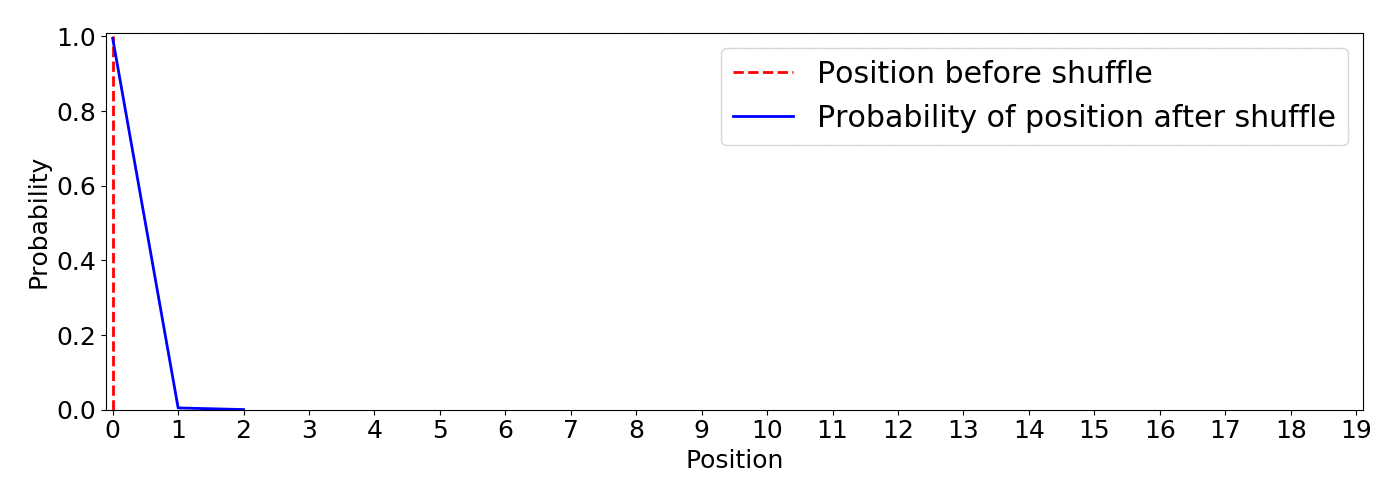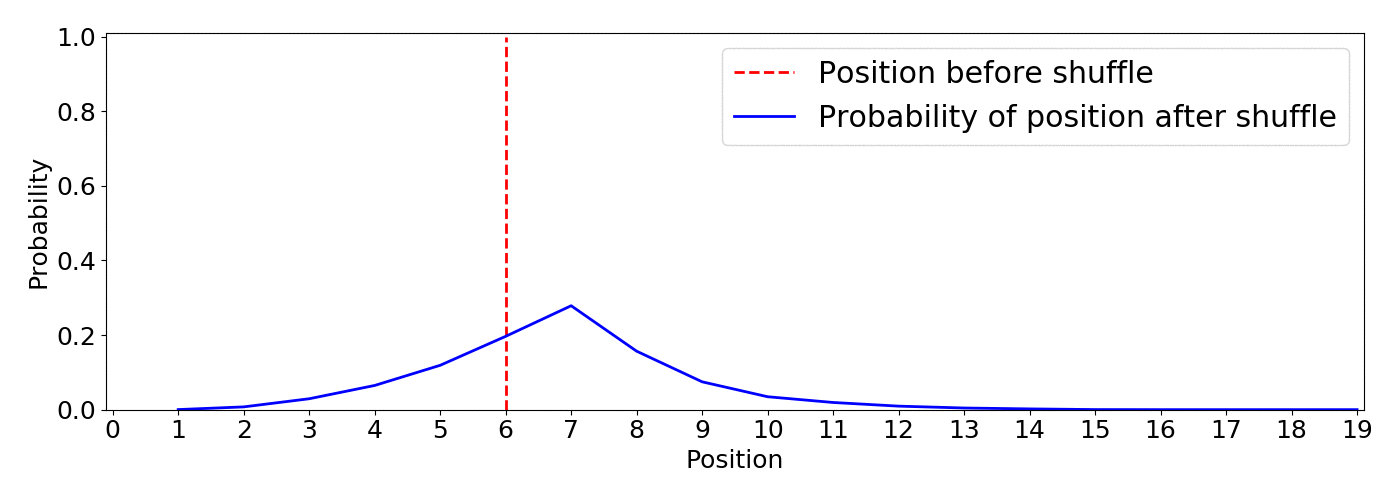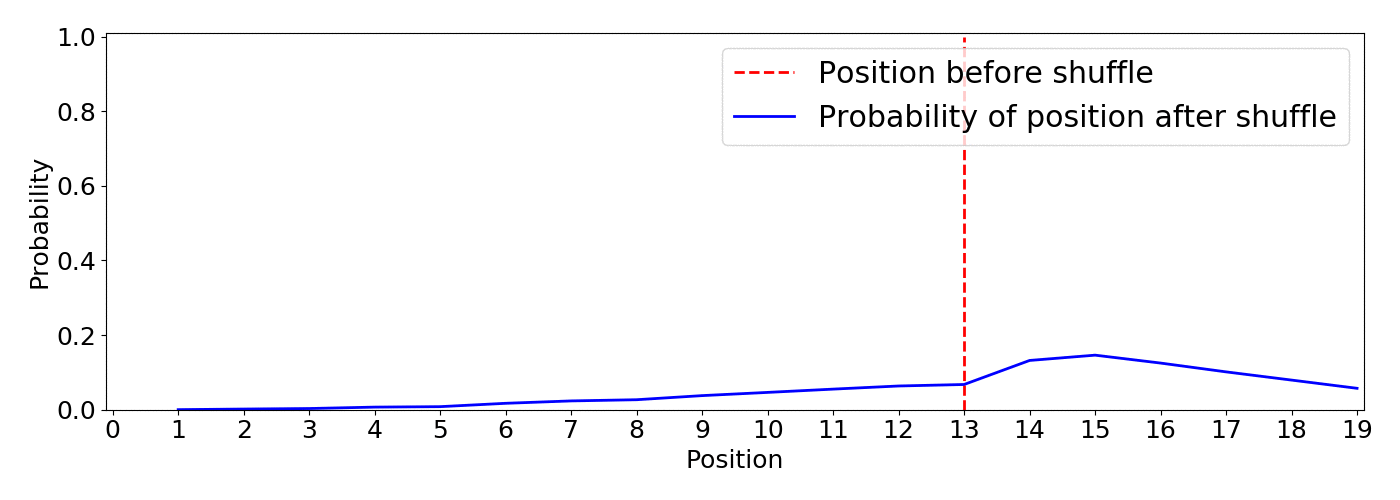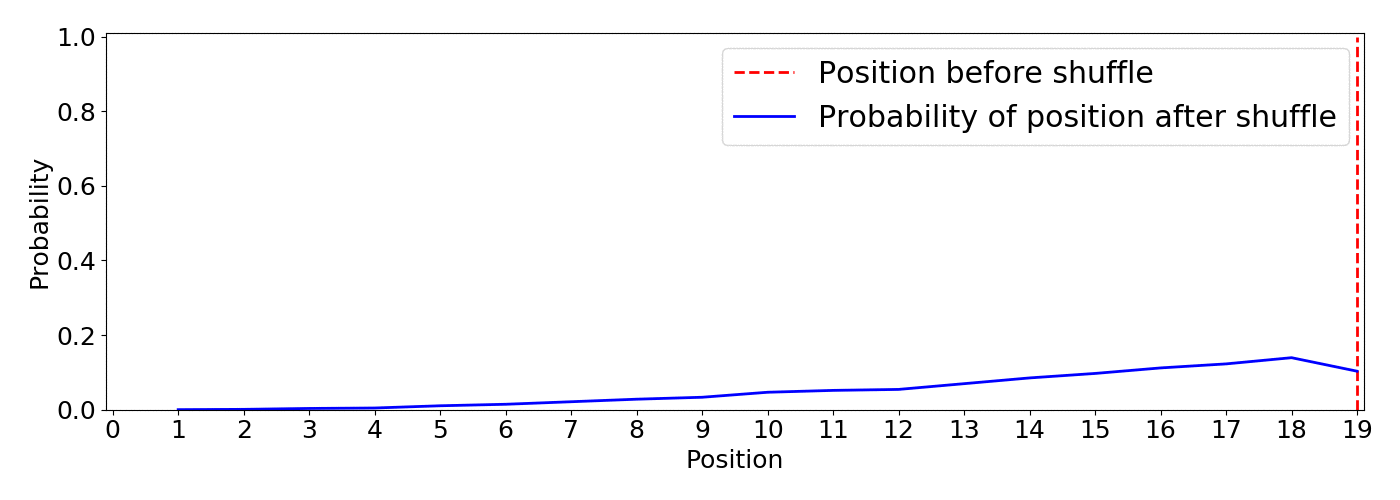
This shuffle method uses the optimized Fisher–Yates algorithm introduced by Richard Durstenfield in 1964 which reduced the running time from (O(n^2)) to (O(n)). By default the algorithm produces a uniform shuffle of an array in which every permutation is equally likely. This means that an item has equal probability to end up in any position.4 Below you can find an animation of the results of the random.shuffle default algorithm. I show the initial position of an item in red and the expected probability distribution of landing in any position after 5000 shuffling simulations.
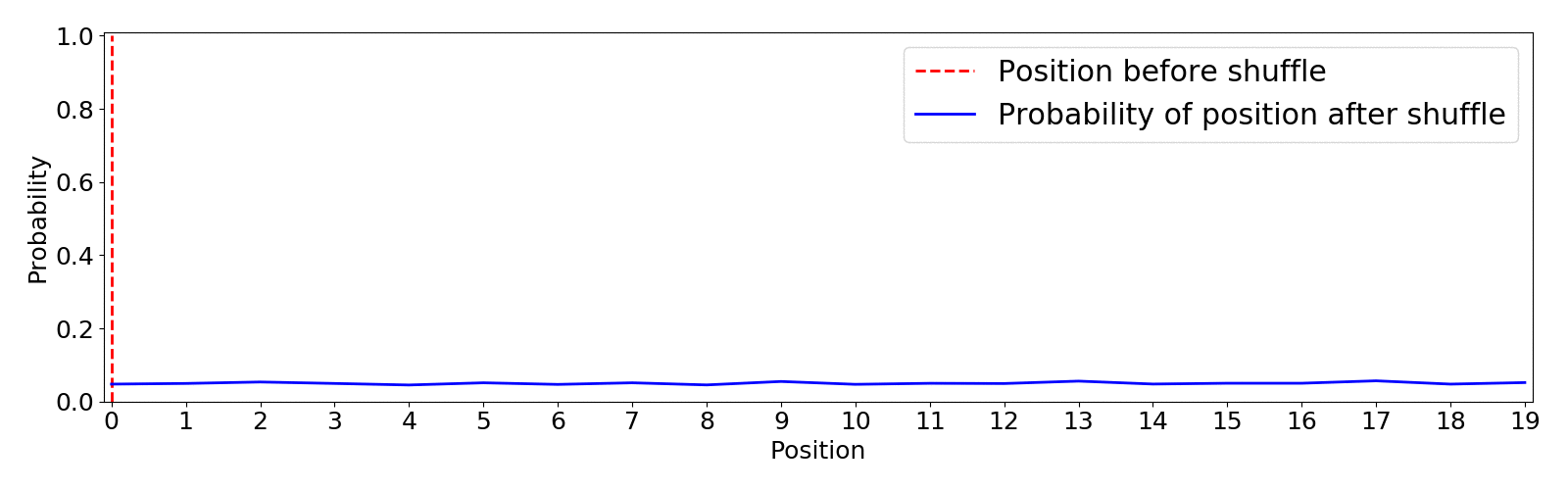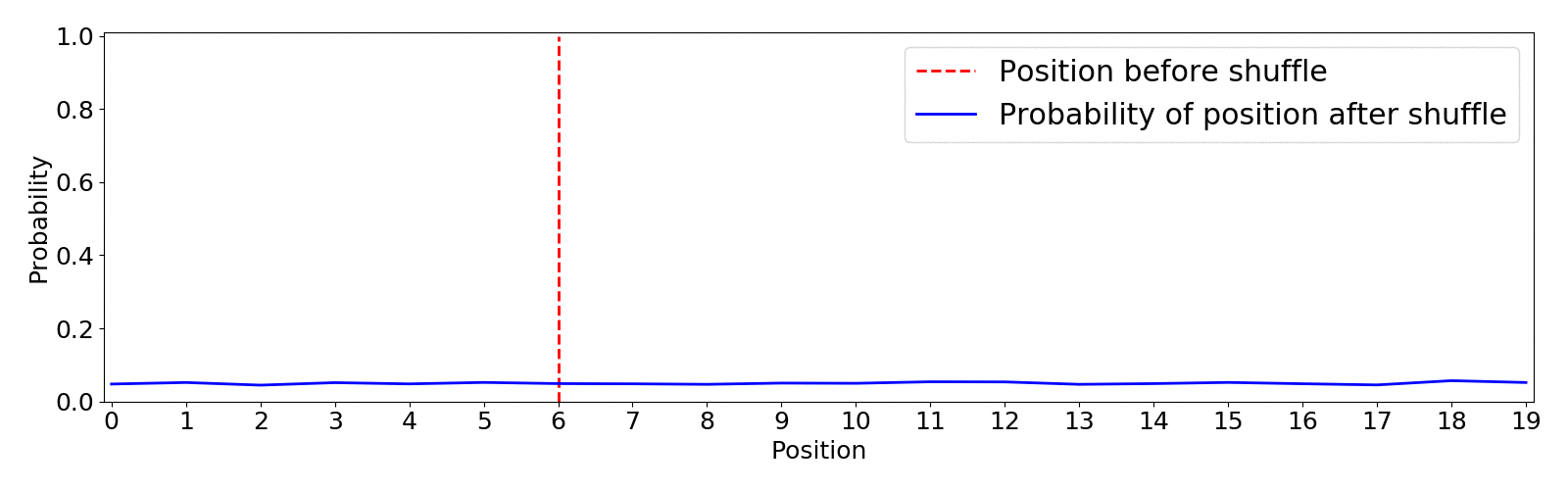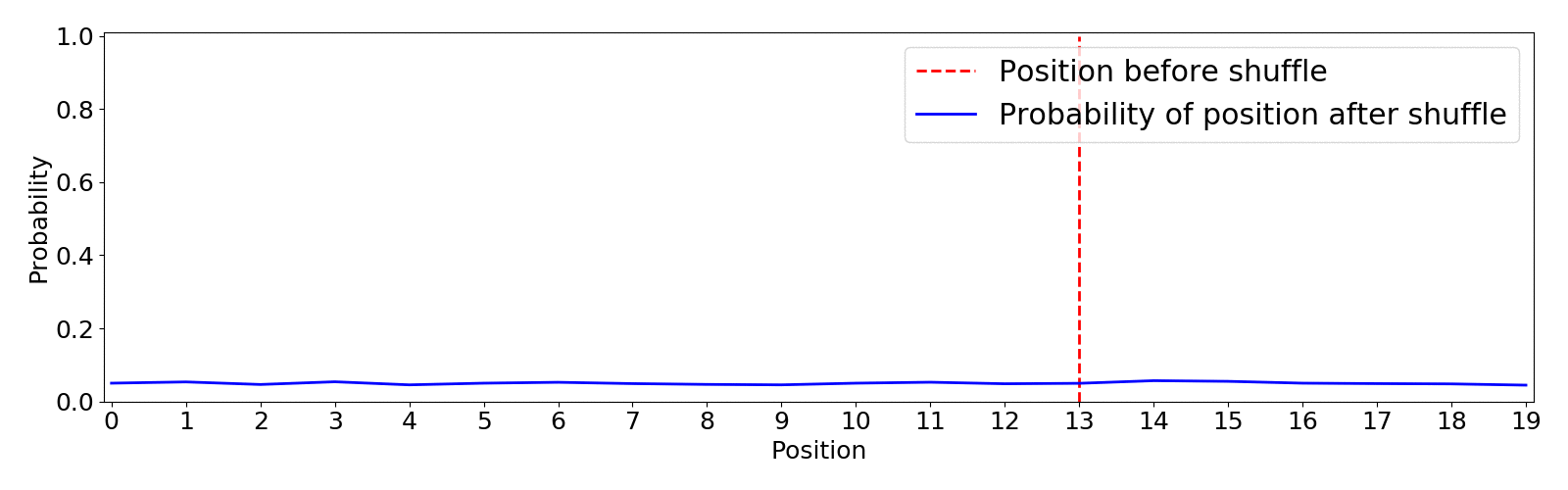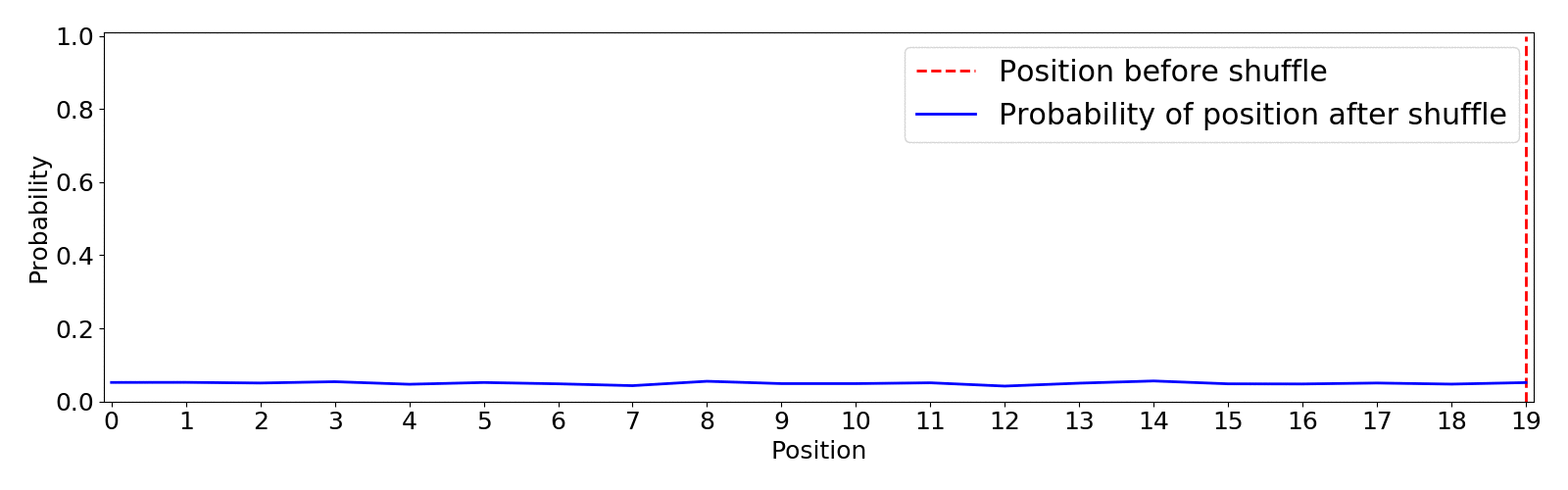
This type of shuffle is not beneficial for our purpose as there is the same probability of the least recommended item to appear on top than any other, this is definitely not the way to go since we can end up with very poor recommendations on top.
Fisher–Yates shuffle / non-uniform
Notice that the shuffle function shown above has the parameter random which is described in the docstring as follows:
def shuffle(self, x, random=None): """Shuffle list x in place, and return None. Optional argument random is a 0-argument function returning a random float in [0.0, 1.0); if it is the default None, the standard random.random will be used. """
If you try to understand the Fisher-Yates algorithm and then look at the source code, you notice that the random parameter affects the location where intermediate swaps will happen and that the effect of a non-uniform random distribution parameter is quite difficult to predict. It kept my mind busy for some hours.
I tried different functions to pass to the random parameter but they all behaved strange and unexpected in one way or another, for example let’s try a (beta) distribution such that the first draws are very likely to be swapped with elements at the end (higher probability near 1.0).5
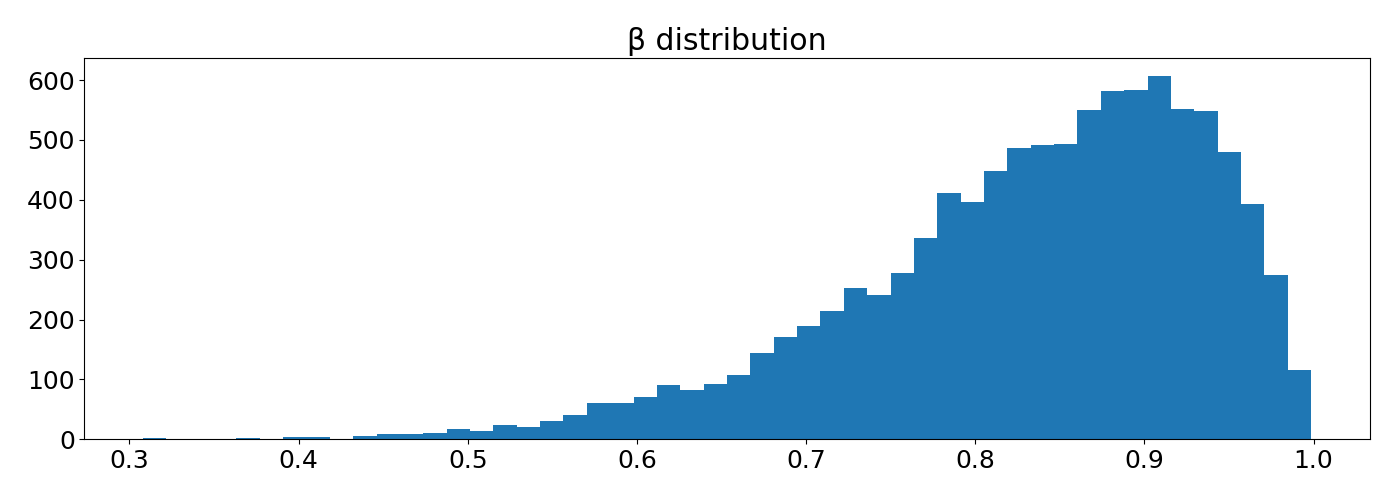
The simulation below uses the (beta)-distribution as the random parameter. This approach does allocate higher probabilities towards higher positions for higher initially ranked items, but the distribution is highly non-symmetrical and very different for different initial positions. I find it surprising that at some point the initial position does not have the maximum probability.6 Also, I find it very hard to explain the relation between the given (beta)-distribution and the resulting probability distribution . I played with the parameters and other distributions but still noticed strange behavior. This will make it quite difficult to explain the expected impact on the recommended items to the user.
Elitist shuffle
This is actually a simple approach, I shuffle the items by choosing items with a weighted probability (this is the same as sampling from a multinomial distribution without replacement). I won’t go into the details but the function numpy.random.choice with the parameter replace=False does what we want, it is just a matter of choosing the appropriate weight probabilities. In this case I choose to set the weights by transforming the reverse position as np.linspace(1, 0, num=len(items), endpoint=False).7 Then I introduce a parameter called inequality as a knob to tune the weight probability difference between positions.
>>> print(inspect.getsource(elitist_shuffle)) def elitist_shuffle(items, inequality): """Shuffle array with bias over initial ranks A higher ranked content has a higher probability to end up higher ranked after the shuffle than an initially lower ranked one. Args: items (numpy.array): Items to be shuffled inequality (int/float): how biased you want the shuffle to be. A higher value will yield a lower probabilty of a higher initially ranked item to end up in a lower ranked position in the sequence. """ weights = np.power( np.linspace(1, 0, num=len(items), endpoint=False), inequality ) weights = weights / np.linalg.norm(weights, ord=1) return np.random.choice(items, size=len(items), replace=False, p=weights)
As the simulation below shows, this approach gives a clearer picture of what’s going on and it let us tune the algorithm using the inequality parameter according to the requirements of our application. This is an animation based on 5000 simulations with inequality=10
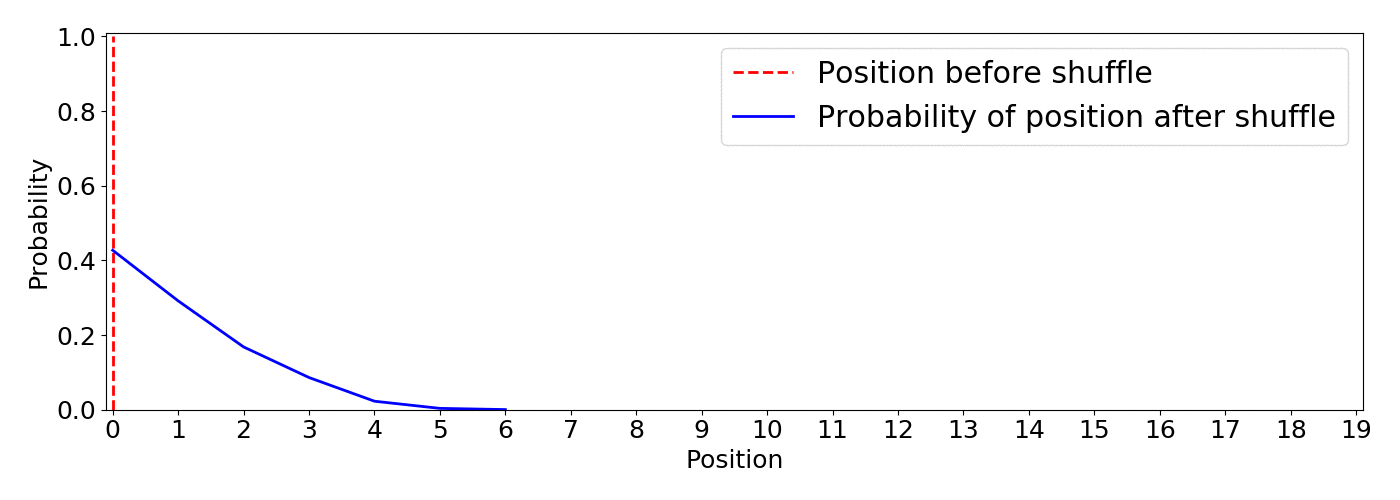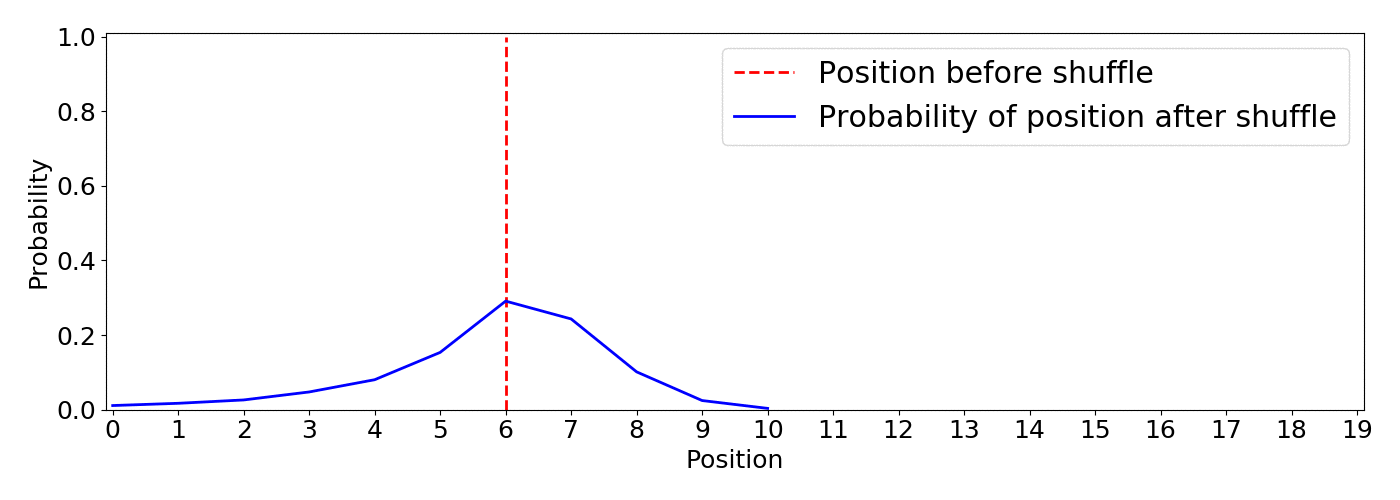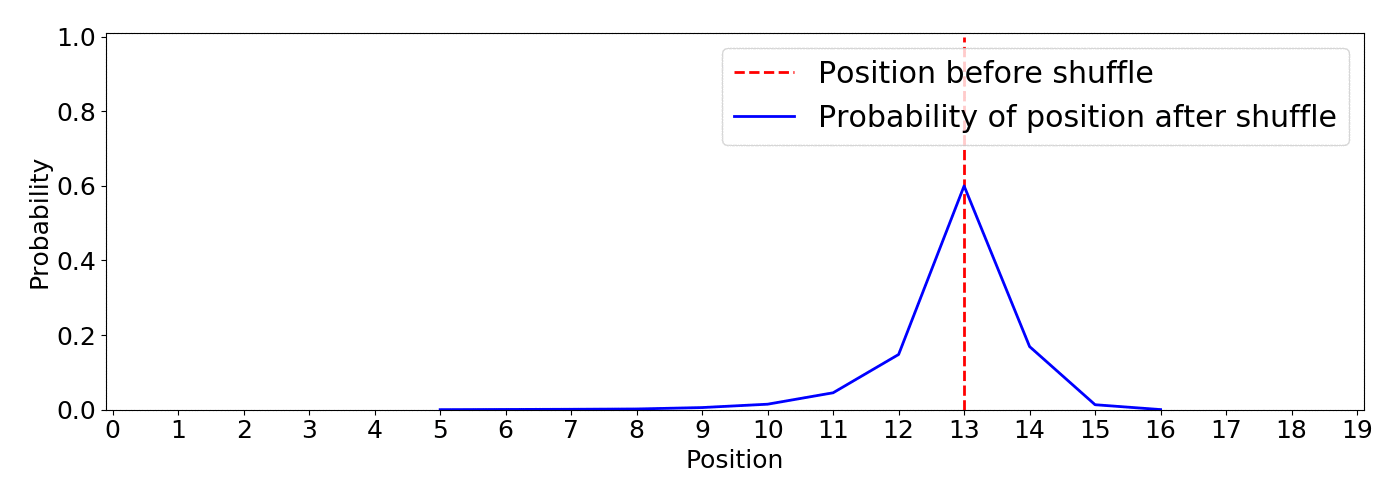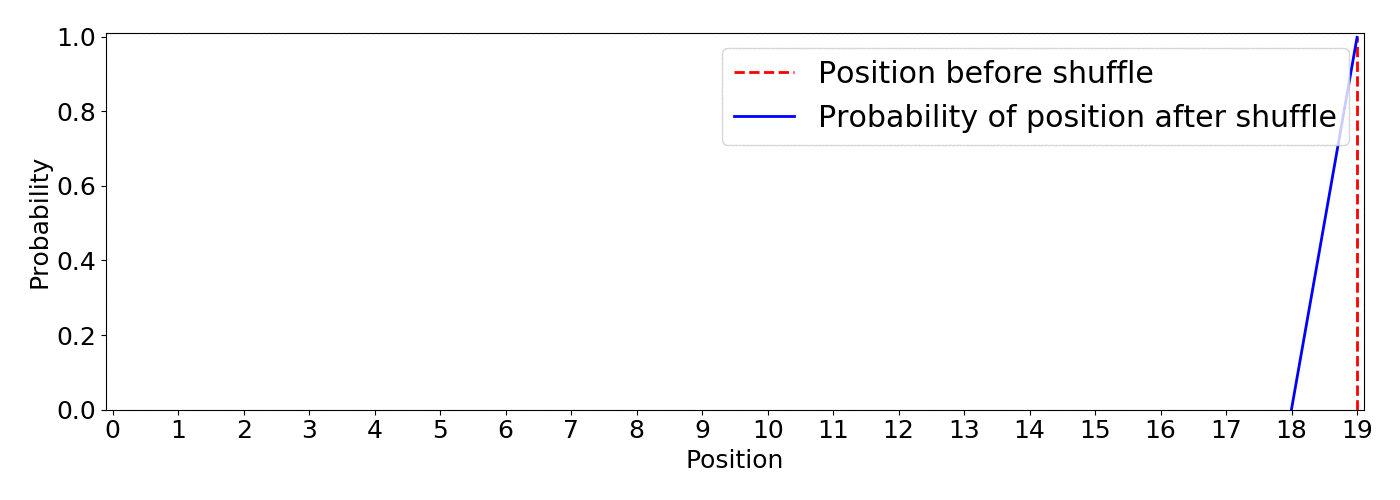
From the animation we notice:
- The maximum probability remains on the initial position.
- Probability decays monotonically with the distance from the initial position.
- The distribution is non-symmetrical but smoother than the previous example.
- Higher ranked items have a higher chance of being moved from their initial position.
A big win is that the inequality parameter has a direct understandable impact on the resulting distributions, want higher items to be more probable to remain on top? Increase inequality. In addition, the behavior translates into the desired functionality:
- Top content would still be relevant after shuffle.
- Content is not the same.
- Some content has changed position.
- Some new content has appeared.
Drawback
The elitist_shuffle function is much slower than np.random.shuffle, but still fast for a common application. Coming back to the example scenario where the items to shuffle are 100, the elitist_shuffle function takes around 1.8ms.
If this is too slow for you I would recommend to first try numba with the no_python parameter enabled and then if necessary try a Cython implementation.
Learn how to build recommender systems
Join us for an extensive one-day course on Recommender Systems and learn how to build your own recommender systems that drives sales and customer satisfaction.
Adiós
As final remarks, I advise you to:
- First, discuss with your team if you need a feature like this. There are applications where the user might be expecting to find the same items it saw last time. Perhaps trigger this behavior if more than x seconds have passed.
- Add the recommendation system scores to the calculation of the weight probabilities. This could just be setting the weights to the scores before the exponentiation and (l^1) normalization .

As always I’m happy to discuss and answer any questions, just ping me on twitter @rragundez.
You can find the code here.
- Some other user similar to me might have done some actions that affect my recommendations, or simply not clicking on the items affects my own recommendations. ↩
- There can be an exploration-exploitation step after. ↩
- It can also be a dynamic threshold based on the scores from the recommendation system. ↩
- This algorithm is also used by numpy. ↩
- This is what we want since the algorithm first swaps elements from the end (look at
reversedin line 303. ↩ - It is not a matter of increasing the number of simulations. I did that and found the same behavior. ↩
- You might be tempted to use
np.arange(len(items), 0, step=-1)which is not numerically robust for a biginequalityparameter. ↩





